




Výukové materiály ZŠ Kaplice, Školní 226





Ze zadání platí SXYZ : SYBCZ = 1 : 2. Pokud obsah trojúhelníku XY Z označíme S, je obsah čtyřúhelníku YBCZ roven 2S, viz obrázek
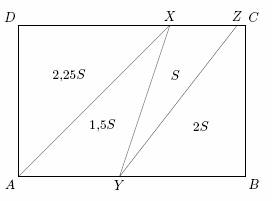
Dále je zadáno SAXY : SYBCX = 1 : 2 a z předchozího plyne, že obsah čtyřúhelníku YBCX
je 2S + S = 3S.
Obsah trojúhelníku AXY tedy musí být 3S : 2 = 1,5S.
Ze zadání také známe SAXD : SABCX = 1 : 2.
Obsah čtyřúhelníku ABCX je 2S + S + 1,5S = 4,5S.
Obsah trojúhelníku AXD je tedy 4,5S : 2 = 2,25S.
Hledaný poměr SAXD : SAXZY je
2,25S : (1,5S + S), tj. 2,25 : 2,5.
Po rozšíření čtyřmi dostaneme poměr 9 : 10.