Výukové materiály ZŠ Kaplice, Školní 226

Řešení příkladu IVa - 7

Obarvěme jednotlivé strany dílků následovně: nejdelší stranu zeleně, s ní rovnoběžnou stranu modře, na ně kolmou stranu žlutě a zbývající stranu červeně; délky odpovídajících stran budeme značit zkráceně z, m, ž a č. Dále označme vybrané „vrcholy“ jednotlivých dílků jako na následujícím obrázku:

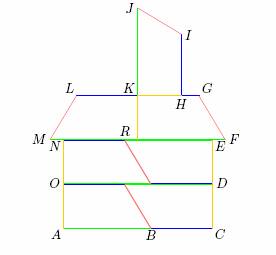
Obvod obrazce je tvořen:
• 3 modrými úsečkami BC, HI a KL, jejichž délky jsou m,
• 2 zelenými úsečkami AB a JK, jejichž délky jsou z,
• 4 žlutými úsečkami CD, DE, NO a OA, jejichž délky jsou ž,
• 3 červenými úsečkami FG, IJ a LM, jejichž délky jsou č,
• 2 shodnými úsečkami EF a MN a 1 úsečkou GH, jejichž délky zatím neznáme.

Délky úseček MN a EF spolu se zelenou stranou ER a modrou stranou RN dávají úsečku MF, která je tvořena dvěma zelenými stranami. Jinými slovy,

|EF| + |MN| = z + z - (z + m) = z - m.

Délku modré strany KG můžeme vyjádřit jako součet délek žluté strany KH a úsečky GH, tedy

|GH| = m - ž

Dohromady, obvod obrazce je

3m + 2z + 4ž + 3č + (z - m) + (m - ž) = 3m+ 3z + 3ž + 3č = 3(m + z + ž + č).

Dostali jsme tak trojnásobek obvodu jednoho čtyřúhelníkového dílku, tedy obvod celého obrazce je roven

3 • 17 = 51 (cm).

Poznámka. Pokud nejprve posuneme některé části obrazce tak, aby obvod zůstal zacho- ván, mohou se některé úvahy zjednodušit, viz např. následující obrázek.

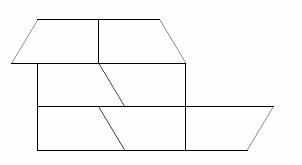
Jiné řešení. Oddělme „komíny od „střechy“ a „střechu“od „zdí“ tak, jak ukazuje obrá- zek.

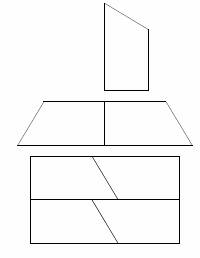
Součet obvodů těchto tří útvarů určíme snadno (použijeme značení m, z, ž, č jako výše):

5m+ 5z + 5ž + 3č

. Uvedený součet je oproti obvodu původního útvaru větší o dvě délky ž, což způsobilo oddělení „komínu“, a o dva součty délek m + z, což způsobilo oddělení „zdí“. Obvod původního útvaru je tedy

(5m+ 5z + 5ž + 3č) - ž - ž - (m+ z) - (m+ z) = 3m+ 3z + 3ž + 3č.

Vidíme, že původní útvar má třikrát větší obvod než čtyřúhelníkový dílek, tj. 3 • 17 = = 51 (cm).