




Výukové materiály ZŠ Kaplice, Školní 226





Ze zadání příkladu je zřejmé, že kosočtverec se rozdělí na čtyři shodné pravoúhlé trojúhelníky o stranách 10, 8 a 6 cm. Jejich složením máme vytvořit postupně trojúhelník, čtyřúhelník a pětiúhelník o maximálním možném obvodu. Úlohu lze řešit zpočátku pokusně a teprve po určitých zkušenostech činit jisté obecnější závěry.
Následující obrázky ukazují možná řešení.
a)
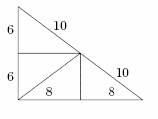
Obvod je 8+8 + 10+10 + 6+6 = 48cm.
b) Lze uvažovat i nekonvexní čtyřúhelníky.
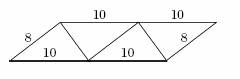
Obvod je 10 + 10+ 8 + 10+10+8 = 56cm.
c) Lze uvažovat i nekonvexní pětiúhelníky.
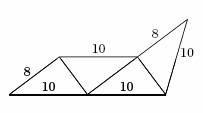
Obvod je 10 + 10+ 10 + 8 + 10+8 = 56cm.