




Výukové materiály ZŠ Kaplice, Školní 226





Nejprve si vypočítáme velikosti zbývajících úhlů. Součet vnitřních úhlů v libovolném čtyřúhelníku je roven 360°, tedy α + β + γ + δ = 360°, po dosazení ze zadání dostáváme 90° + (δ + 100°) + 90° + δ = 360°, odtud δ = 40° a β = 140°. Nyní si budeme všímat pouze trojúhelníku ACD (obr.). Ten je rovnoramenný se základnou AC, jak vyplývá ze zadání. Zjistíme tedy velikost úhlu ? při základně. Platí: 180° = 40° + 2ω, velikost úhlu při základně tedy je 70°.
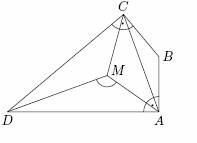
ΔAMD: vnitřní úhel při vrcholu A má velikost 70° : 2 = 35°, vnitřní úhel při vrcholu D má velikost 40° : 2 = 20°. Velikost vnitřního úhlu při vrcholu M je rovna 180°- 35° - 20° = 125°.