




Výukové materiály ZŠ Kaplice, Školní 226





Používáme-li značení dle obrázku, mají úhly zmiňované v zadání tyto velikosti: 20°,
Γ, Δ, 20° + Γ, Γ + Δ, 20° + Γ + Δ.
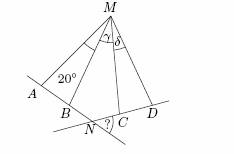
Prověříme všechny možné velikosti 20° + γ.
1) Předpokládejme, že 20° + γ = 50°. Pak γ = 30°.
Některá z neznámých velikostí úhlů musí být dle zadání 20°,
připadá v úvahu pouze δ = 20°.
Spočítáme velikosti všech zmiňovaných úhlů a dozvíme se, že odpovídají zadání.
2) Předpokládejme, že 20° + γ = 70°. Pak γ = 50°.
Některá z neznámých velikostí úhlů musí být dle zadání 20°, připadá v úvahu pouze δ = 20°.
Zmiňovaná šestice úhlů má tak tyto velikosti: 20°, 50°, 20°, 70°, 70°, 90°,
což je v rozporu se zadáním.
3) Předpokládejme, že 20°+ γ = α.
Ze zmiňovaných úhlů je největší úhel 20°+ γ + δ, proto musí být roven 70°.
Pak Γ + Δ = 50°. Pro úhly γ, δ však v zadání nelze najít takové velikosti,
aby byla předchozí rovnost splněna. Docházíme k jedinému řešení: γ = 30°, δ = 20°.
Trojúhelník MAB je rovnoramenný, proto |∠ABM| = (180° - 20°) : 2 = 80°.
Vedlejší úhel MBN má velikost |∠MBN| = 180° - 80° = 100°.
Obdobně přes výpočet úhlů v trojúhelníku MDC dojdeme k velikosti úhlu |∠MCN| = 100°.
Velikost vnitřních úhlů čtyřúhelníku MBNC je 360°, proto |∠BNC| = 360° - 30° - 100° - 100° = 130°.
Vedlejší úhel k tomuto úhlu má velikost 50°, přímky AB a CD tedy svírají úhel 50°.