




Výukové materiály ZŠ Kaplice, Školní 226





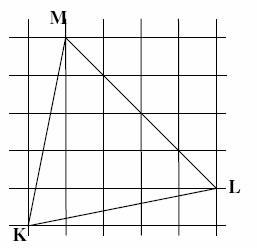
Vypočítejte obsah trojúhelníku KLM, jestliže čtverce čtvercové sítě mají stranu dlouhou 2 cm.
(řešení)

Vybarvený obrazec ve čtvercové síti na obrázku má obvod 40 cm. Jaký je jeho obsah?
(řešení)

Vypočítejte obsah vybarvené plochy BEDF, jestliže obdélník ABCD má rozměry 10 cm a 6 cm a body E, F jsou středy úseček BC, AD.
(řešení)
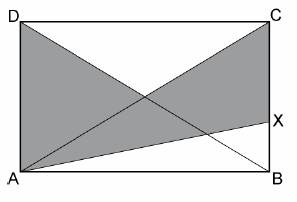
Vypočítejte obsah vybarvené části obdélníku ABCD, jestliže |AB| = 10 cm, |BC| = 6 cm,
|BX| = 1/3 |BC|.
(řešení)
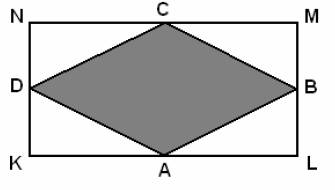
Body A , B, C, D jsou středy stran obdélníku KLMN s rozměry 6 cm a 3 cm. Vypočítejte obsah
vybarveného obrazce.
(řešení)
Body E, F, G, H jsou středy stran čtverce ABCD, jehož obvod je 96 cm, a body
K, L, M, N jsou středy stran čtverce EFGH. Vypočítejte obsah čtverce KLMN
(řešení)

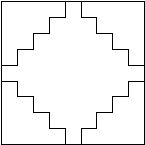
Franta měl papír tvaru čtverce o obsahu 100 cm2. Vystřihl z něho tento útvar:
Stříhal tak, aby byl útvar co největší.
Míša měl větší papír, proto s ním nemusel tolik šetřit. Stříhal takto:
Získal stejně velký útvar jako Franta. Jak velký obsah měl Míšův papír?
(řešení)
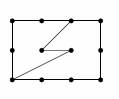
Na obrázku je znázorněn pětiúhelník a šestiúhelník s vrcholy v mřížových bodech
čtvercové sítě. Urči obsah šestiúhelníka, víš-li, že pětiúhelník má obsah 7,5 cm2 .
(řešení)
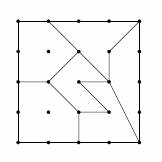
Na obrázku vidíte čtverec rozdělený na šest mnohoúhelníků. Všechny tyto mnohoúhelníky
mají vrcholy v mřížových bodech čtvercové sítě a největší z nich má obsah 35mm2.Zjistěte obsah celého čtverce.
(řešení)
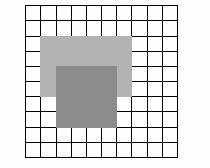
Kamilka při kreslení obdélníků ve čtvercové síti narazila na takovouto zajímavou
dvojici: Obdélník s rozměry 6 cm a 4 cm a čtverec se stranou délky 4 cm. Nejdříve
zakreslila do sítě obdélník a pak čtverec (obr.). S údivem ve svém obrázku objevila,
že obsah nezakryté části obdélníku je roven obsahu čtverce a že nezakrytá část obvodu
obdélníku je rovna celému obvodu čtverce. Mezi následujícími obdélníky najdi
všechny dvojice, které mají obě vlastnosti Kamilčiných obdélníků: 3 x 9 , 4 x 9 ,
4 x 6 a 5 x 7 (v centimetrech)
(řešení)