




Výukové materiály ZŠ Kaplice, Školní 226





Na kolik nepřekrývajících se částí je možné rozdělit rovinu čtyřmi různými přímkami?
Určete všechny možnosti a každou z nich znázorněte graficky.
(řešení)
Narýsujte dva libovolné obdélníky tak, aby jejich průnik byl a) osmiúhelník, b) sedmiúhelník, c) šestiúhelník, d) pětiúhelník, e) čtyřúhelník, f) trojúhelník, g) úsečka,
h) bod. V případech a) až f) společnou část obdélníků vyšrafujte.
(řešení)
Je dán rovnoběžník ABCD: ?AB? = 9 cm, ?BC? = 6cm, velikost úhlu DAB je 60°.
Rozdělte daný rovnoběžník na 6 shodných trojúhelníků.
(řešení)
Je dán pravoúhlý trojúhelník s přeponou délky 8 cm a jednou odvěsnou délky 4 cm.
Zjistěte, zda ze 6 takovýchto nepřekrývajících se trojúhelníků se dá složit rovnoběžník, jehož
jeden vnitřní úhel je 30°. Zjistěte všechny možnosti
(řešení)
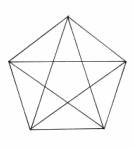
Spočtěte všechny trojúhelníky na obrázku.
(řešení)
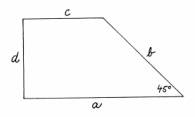
Pravoúhlý lichoběžník (jestliže druhý úhel při základně a je 45° a c = d) na obrázku rozdělte
na 4 shodné lichoběžníky.
(řešení)
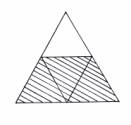
Na obrázku vidíte, jak je možné rozdělit rovnostranný trojúhelník na 4 shodné části.
Odstraňme vrchní trojúhelník a trojúhelníky, které zůstaly, vytvoří lichoběžník,
jehož ramena a menší základna jsou stejné.Zkuste tento lichoběžník rozdělit na 4 shodné části..
(řešení)
Rozdělte pravidelný šestiúhelník na 12 shodných čtyřúhelníků.
(řešení)
Úhlopříčky dělí kosočtverec s obvodem 40 cm na čtyři trojúhelníky s celočíselnými délkami stran,
z nichž každý má obvod 24 cm. Jaký největší obvod může mít
a) trojúhelník,
b) čtyřúhelník,
c) pětiúhelník
složený z těchto trojúhelníků? (Trojúhelníky se nesmějí překrývat a všechny čtyři je třeba použít.)
(řešení)
Osově souměrný pětiúelník s obsahem 27 cm2 má právě tři vnitřní úhly pravé
a právě tři strany shodné. Zjistěte velikosti dalších dvou vnitřních úhlů pětiúhelníka
a déku některé z trojice shodných stran.
(řešení)