Výukové materiály ZŠ Kaplice, Školní 226





Nádrž má tvar kvádru s rozměry dna 2 m a 5 m. Jakou nejmenší hloubku musí tato nádrž mít, aby se do ní dal přečerpat všechen benzin z plné nádrže tvaru krychle s délkou hrany 2 m?
Velká krychle je slepena z osmi stejných malých krychliček. Povrch malé krychličky je 24 cm2. Jaký povrch má velká krychle?
Dostali jsme krychli, která měla délku hrany vyjádřenou v centimetrech celým číslem.
Všechny její stěny jsme obarvili na červeno a poté jsme ji rozřezali beze zbytku na krychličky o hraně 1 cm.
Lukáš tvrdí, že krychliček se dvěma obarvenými stěnami je desetkrát více než těch se třemi obarvenými stěnami.
Martina říká, že krychliček se dvěma obarvenými stěnami je patnáctkrát více než těch se třemi obarvenými stěnami.
Pravdu má však pouze jeden — kdo? A kolik měřila hrana původní krychle?
Na obrázku je krychle o hraně 2 cm tvořená osmi krychličkami s hranou 1 cm. Osm stěn krychliček je obarveno černě, ostatní jsou bílé. Přitom z nich lze složit krychli, jejíž povrch je bílý. Kolika způsoby mohou být krychličky obarveny? Předpokládejte, že stejně obarvené krychličky nedokážeme odlišit, mohou se tedy zaměnit.
Krabička tvaru krychle o hraně 4 cm je zcela naplněna srovnanými hracími kostkami, krychličkami s hranou délky 1 cm. Vymyslete všechny různé krabičky tak, aby měly čtvercové dno a do každé z nich se všechny kostky přesně vešly. Napište jejich rozměry.
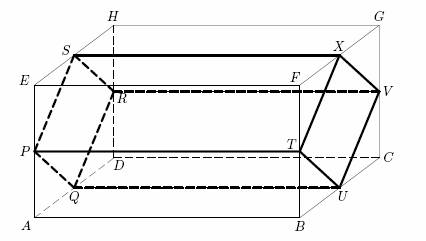
V kvádru ABCDEFGH je umístěno těleso PQRSTUVX, jehož vrcholy jsou středy hran kvádru, viz obrázek. Vypočtěte objem a povrch tělesa, je-li: |AB| = 8 cm, |BC| = 6 cm, |BF| = 4 cm.
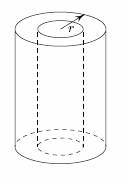
Středem rotačního válce s podstavou o poloměru r a výškou v byl vyvrtán válcový otvor. Objem takto vzniklého „dutého válce“ je poloviční než objem válce původního. Vyjádřete tloušťku stěny dutého válce pomocí r.
Z krychliček o hraně 1 cm jsme postavili kvádr. Kdybychom z kvádru odebrali jeden sloupec, zbytek stavby by se skládal z 602 krychliček. Pokud bychom místo toho odebrali jeden řádek horní vrstvy, zůstala by nám stavba z 605 krychliček. Jaké má kvádr rozměry?
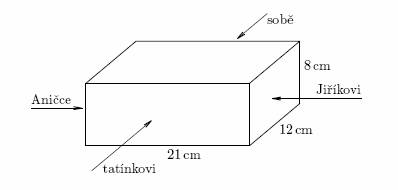
Maminka má v lednici cihlu sýra, která je znázorněná na obrázku. Postupně z ní odřezává 1 cm silné plátky na smažení. Nejprve odřízla zepředu plátek s rozměry 21 cm, 8 cm, 1 cm pro tatínka. Pak z boku odřízla pro Jiříka, zezadu pro sebe a nakonec z druhého boku pro Aničku. Napiš, jaké rozměry mají jednotlivé plátky. Urči rozměry zbytku sýra.
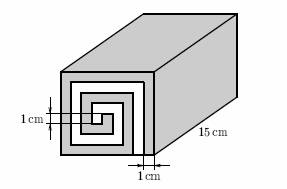
Na obrázku vidíš tzv. kvadroládu (speciální druh rolády).
Je vyrobena z bílé a hnědé marcipánové hmoty, přičemž obě hmoty mají stejnou tloušťku, a to 1 cm.
Celá kvadroláda má délku 15 cm. Prodává se rozkrájená na 10 shodných plátků. Zjisti
a) rozměry jednoho plátku,
b) kolik gramů hnědé hmoty a kolik gramů bílé hmoty je třeba na její přípravu, jestliže víš,
že 1 cm2 marcipánu má hmotnost 2 gramy.